自2018年以来,我们在“从教走向学”的道路上逐步走向深入。我们开展单元教学的设计与实践,拓展基于标准学习的含义与内涵,探寻核心素养落地的方法与路径。
开卷有益,我们广泛阅读和学习理论书籍;智慧众筹,我们共同研讨和优化单元设计案例;深耕课堂,我们从单元设计走向单元教学的实践……
经过一段时间的研究实践的积累,在前段时间的单元教学实践交流活动中,每个学科梳理了丰富的单元设计案例,带来了生动的课堂教学,总结了单元教学实践中的思考与感悟。课程研究院将陆续推出【单元教学实践】系列分享,展示每个学科在单元教学实践中的设计案例、课堂教学与实践智慧。
概念引领教学——小学数学单元探究
在基于标准的学习过程中,我们逐渐从教走向学。通过大概念的提炼,我们达成了教师共识;通过回答核心问题帮助学生打破固有学习方式的束缚;学生通过完成核心任务展现学习的进程。为进一步推进“基于标准的学习”的研究与实践,小学数学学科团队始终走在研究思考的路上。

在研究的过程中,崔晨鹏老师以《等量关系》这节课为例。从足、篮、排三类球重量故事的背景出发,分两次建立等量关系。首次建立等量关系是在学生关注已知信息的前提下,寻找等量关系,在借助模型开展操作的过程中正确地找到并建立等量关系,在解读他人作品的过程中发现未知量对于等量关系的重要性。二次建立等量关系是由学生自行创建等量关系解决问题,这个过程彰显了我校九年一贯制背景下,对于学生创造力的培养。在生生讨论中,一些学生关注到了于课堂初始建立的不等关系,发现限定条件,更合理的创建等量关系。最后,引导学生发现生活中的等量关系,运用等量关系解决问题。
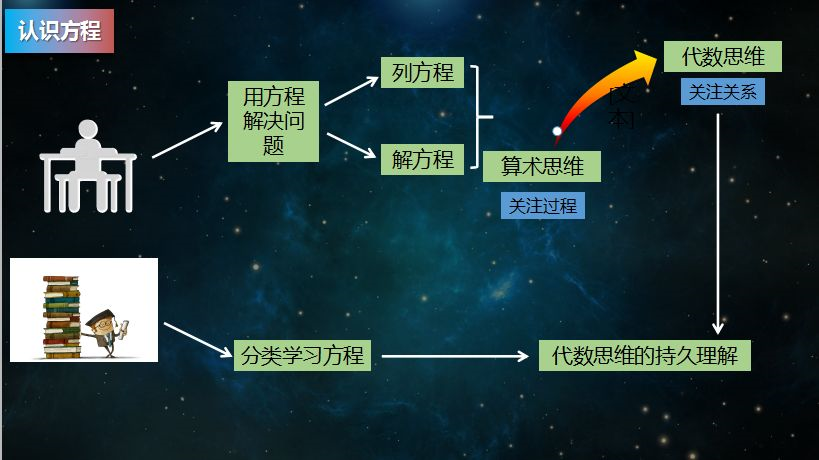
纵观方程单元:字母表示数的重点在于发现并表示规律,发展符号意识;找数量关系是发现并表示关系的过程,而等量关系则最能反映方程本质,基于史宁中老师对方程本质的叙述:方程描述的是现实世界中与数量有关的具有共同点的两个故事,共同点是它们的数量相等;列方程是分析关系的过程;解方程是借助关系,保持关系的过程;猜数游戏是运用关系、深化关系的过程。基于此四年级数学团队教师达成共识:方程是一种关系、一种模型、一种程序。进而提出学科大概念:(1)抽象使数学具有更大的普适性。(2)方程用数学的形式描述现实生活中的等量关系。(3)模型使数学与外部建立联系。从而形成单元学习目标。为了持久理解大概念,彰显知识的本质性与延伸性,提出核心问题:如何理解方程中的变与不变?通过学生的回答我们清楚的看到学生从关注结果的算数思维走向关注关系的代数思维。为了表征核心问题,为单元学习目标的落地寻找评估证据,提出核心任务:利用ax+b=c编写故事。 刘婷婷老师以长方体(一)单元为例解读了大概念的提取过程。提炼大概念的过程中,采用了自下而上的教者思维路径。即基于课标、教材,明确学科素养,提炼知识本质。在解读课程标准的过程中可以发现,从素养方面分析,本单元重点发展学生的空间观念。从知识层面分析,本单元主要是借助低维图形研究高维图形问题。基于上述分析,得到了本单元的学科大概念:图形的基本元素决定了图形的空间表现形式。许园园老师以面积一课为例,分享了核心问题的设计过程。一个好的核心问题,不仅要能够落实单元学习目标,更重要的是能够彰显知识的本质性和迁移性。基于此,许老师从课标出发,纵向梳理长度(一维)、面积(二维)、体积(三维)的测量。得到了测量的基本策略,即统一单位的累加。在梳理教材的过程中发现,关于长度和面积的教学都是先认识长度或面积,统一单位,体会单位的累加再去求不规则图形的长度或面积。这种一致性,启发我们可以通过研究一维线段长度的方法去研究二维面积的大小问题。基于上述分析,得到了核心问题:如何用研究线段长度的方法去解决面积大小的问题?通过学生的作品可以看出,通过回答核心问题能够意识到长度、面积均有单位,对于三维立体图形也有单位。同时,建构了长度-面积-体积的学习路径,为后续学习做好铺垫。李玉东老师以圆柱圆锥单元为例对核心任务展开了论述,基于单元核心问题,设计相应的核心任务:用卡纸制作一个体积为376.8立方厘米的圆柱和圆锥的组合体,并求出大约需要的卡纸面积。始于数据,逆向思考,让学生通过分析、动手操作等方式建立圆柱圆锥知识体系。大概念引领下的单元教学实践,一分校的小学数学团队一直行走在路上,相信在不断接近学科本质的过程中,老师们也将不断成长。









